
Công thức lượng giác là nội dung kiến thức chiếm lượng lớn trong chương trình toán học THPT. Trong đó công thức hạ bậc lượng giác là 1 trong những nội dung quan trọng học sinh không thể bỏ qua. Tuy nhiên lượng kiến thức của phần này khá lớn, đòi hỏi các em phải đầu tư thời gian để ghi nhớ và rèn luyện thành thạo các dạng bài tập. Hãy cùng The Dewey Schools tìm hiểu thông tin đầy đủ, chi tiết để áp dụng trong giải toán về công thức hạ bậc ngay trong nội dung dưới đây nhé.

Công thức hạ bậc là gì?
Lượng giác (Trigonometry) là nội dung thuộc chương trình toán học. Lượng giác sử dụng để tìm hiểu về hình tam giác và sự liên kết giữa cạnh và góc của tam giác. Từ lượng giác chỉ ra hàm số lượng giác, trong đó hàm số lượng giác diễn tả các mỗi liên kết và áp dụng vào các môn học khác.
Hạ bậc là hạ từ bậc cao xuống bậc thấp, trong đó công thức hạ bậc lượng giác là kỹ thuật phổ biến trong toán học sử dụng công thức đưa hàm số lượng giác từ bậc cao xuống bậc thấp hơn. Từ đó chúng ta có thể giải quyết các bài toán phức tạp một cách dễ dàng và chính xác.
Xem thêm: [2023 Update] Tổng hợp công thức lượng giác lớp 10, 11
7 công thức hạ bậc lượng giác cơ bản không thể bỏ qua
Công thức hạ bậc lượng giác giúp hạ bậc hay giảm bớt các hạng tử từ bậc cao xuống bậc thập. Các bước này có tác dụng làm cho bài tập trở nên dễ giải hơn, các phép tính đơn giản và ngắn gọn hơn. Trong chương trình lượng giác của lớp 10, có 10 công thức hạ bậc cơ bản mà học sinh cần nắm vững. Cụ thể:
1. Công thức hạ bậc bậc 2
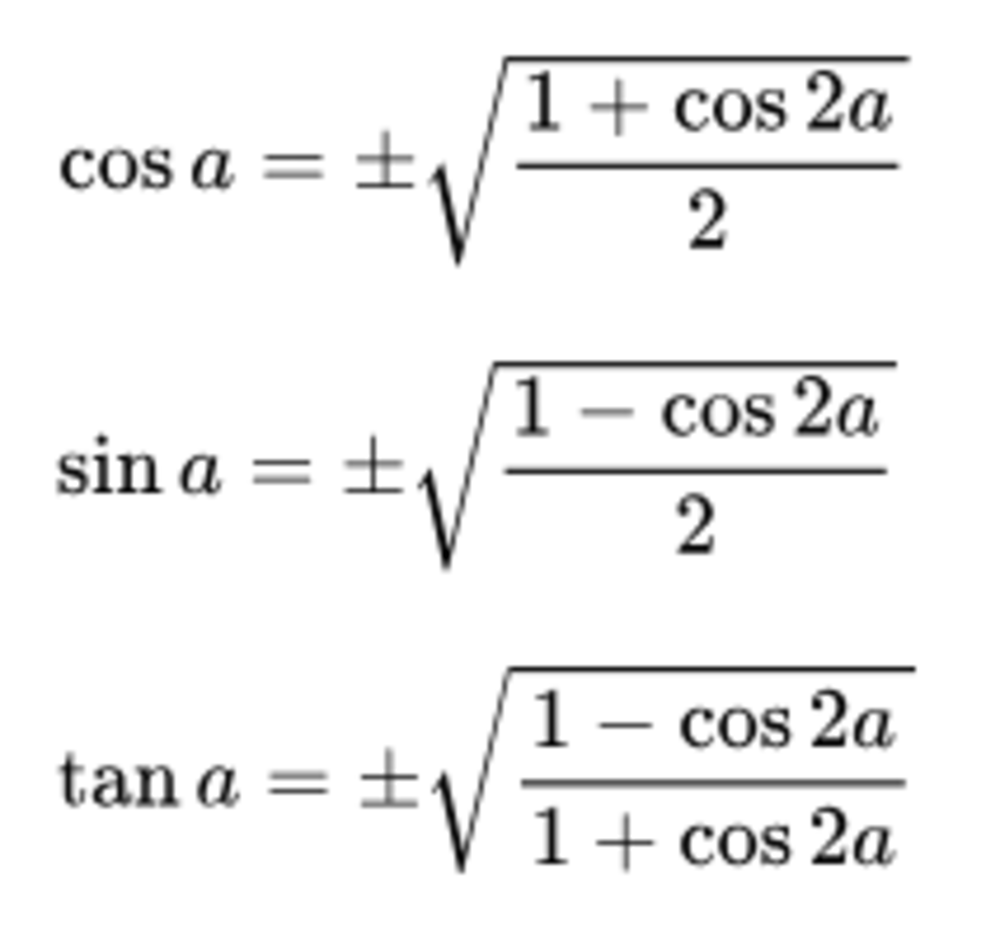
2. Công thức hạ bậc 3
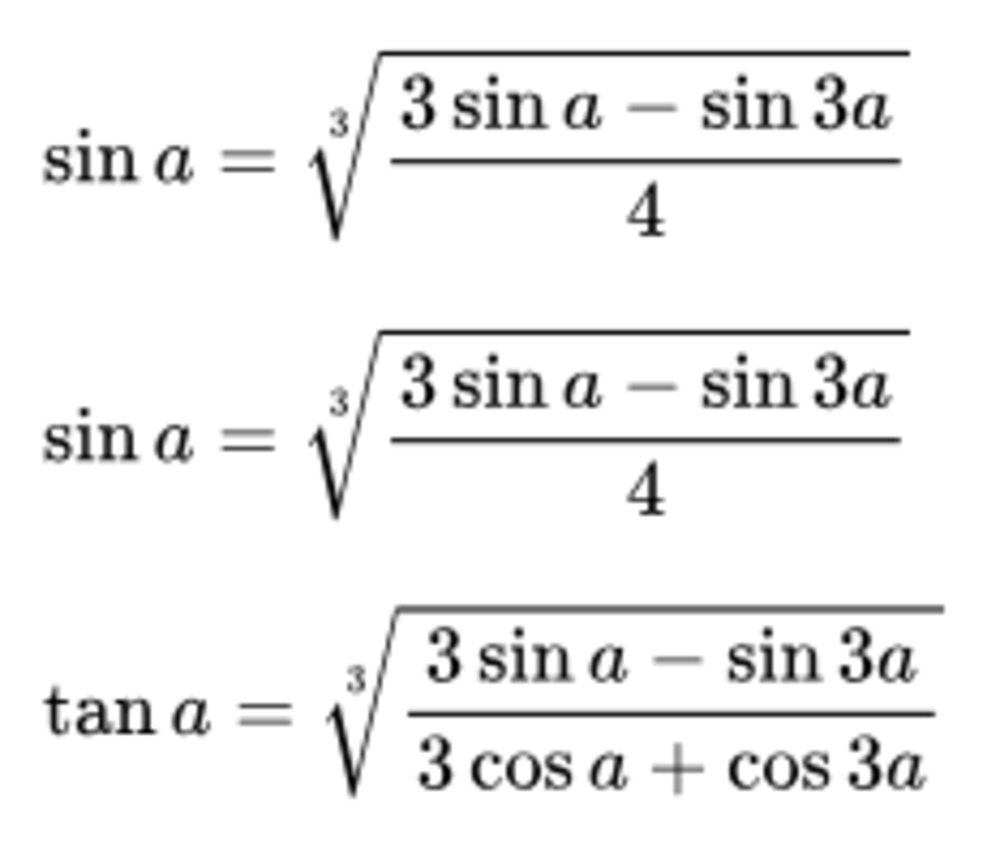
3. Công thức hạ bậc 4
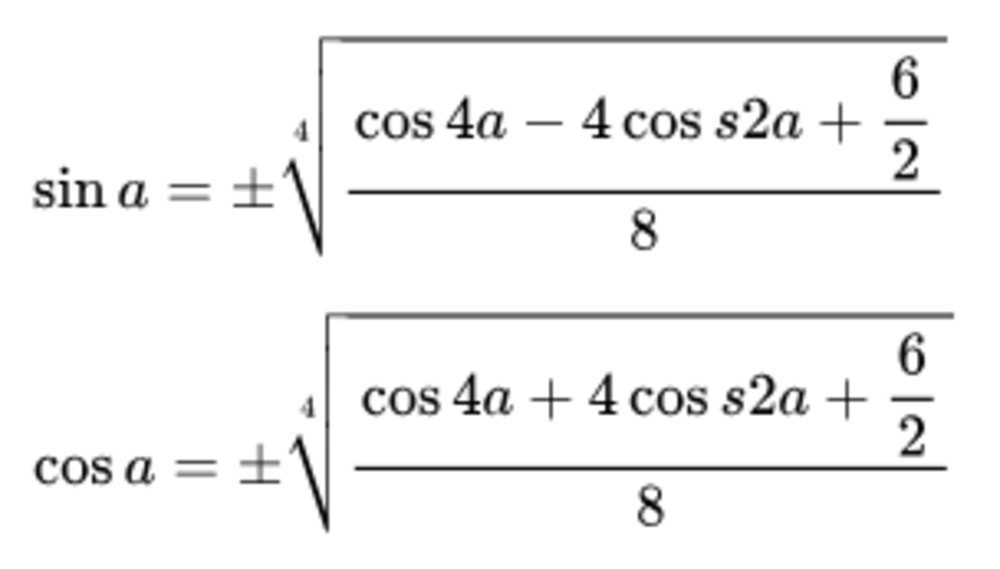
4. Công thức hạ bậc bậc 5

5. Công thức hạ bậc lượng giác 2 – 3 – 4 khác
Công thức hạ bậc sin bậc 2, cos mũ 2, tan mũ 2

Công thức hạ bậc sin, cos mũ 3
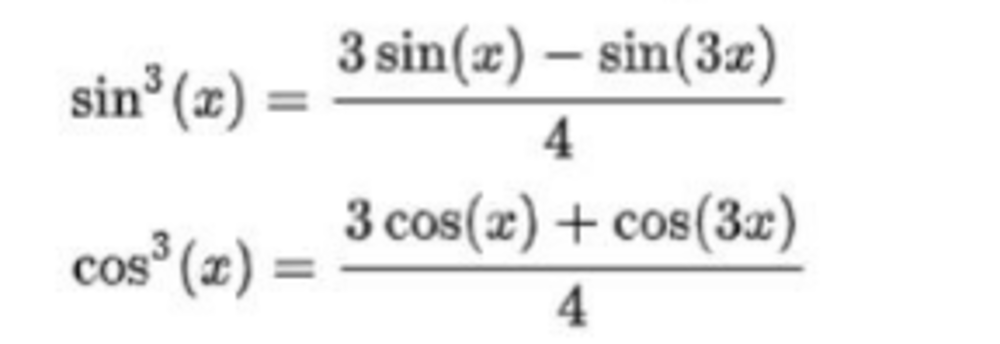
Công thức hạ bậc sin, cos mũ 4

6. Phương pháp hạ bậc toàn cục
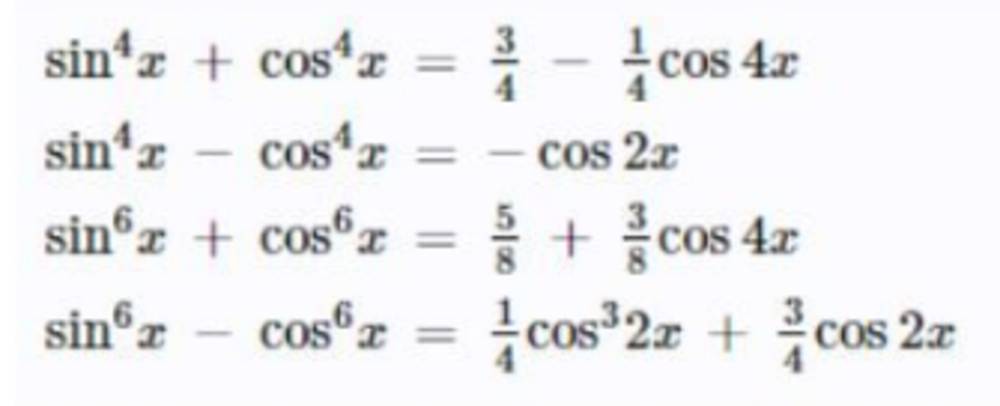
7. Phương pháp hạ bậc lượng giác đối xứng
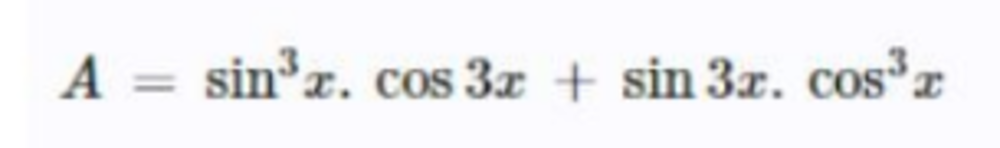
Xem thêm: Tuyển tập kiến thức công thức lượng giác lớp 10 đầy đủ nhất
Ví dụ minh họa công thức hạ bậc lượng giác
Ví dụ 1:
Rút gọn biểu thức sau:
A = sin2x + 2 sin(a-x) . sinx . cosa + sin2(a-x)
= sin2x + sin(a-x) (2sinx cosa + sin(a-x))
= sin2x + sin(a-x) (2sinx cosa + sina cosx – cosa sinx)
= sin2x + sin(a-x) (sinx cosa + sina cosx)
= sin2x + sin(a-x) sin(a+x)
= sin2x + 1/. (cos2x – cos2a)
= sin2x + sin2a – sin2x
= sin2x
Ví dụ 2:
Phương trình biến đổi về dạng:
(1 – cos2x)/2 = (1 + cos4x)/2 + cos23x
=> 2cos23x + (cos4x + cos2x) = 0
=> 2 cos23x + 2cos3x . cosx
=> (cos3x + cosx) cos3x = 0
=> 2cos2x . cosx . cos3x = 0
Ví dụ 3:
Rút gọn biểu thức sau:
B = sin3x . cos3x + sin3x . cos3x
= ¼ . (3sinx – sin3x) cos3x + ¼ (3cosx + cos3x) sin 3x
= ¾ (sinx .cos3x + cosx . sin3x)
= ¾ . sin4x
Ví dụ 4:
sin4x + cos4x
= (sin2x + cos2x)2 – 2. sin2x . cos2x
= 1 – ½ . (2sinx . cosx)2
= 1 – ½ . sin22x
Xem thêm: Cập nhật kiến thức tổng hợp về số hữu tỉ mới nhất 2023
Cách hay ghi nhớ công thức lượng giác
Số lượng công thức lượng giác không nhỏ, chia thành nhiều loại khác nhau khiến nhiều học sinh cảm thấy vô cùng khó nhớ. Tuy nhiên với các mẹo dưới đây các em sẽ gỡ rối hiệu quả vấn đề này. Cùng The Dewey Schools tham khảo các em học sinh nhé:
1. Mẹo ghi nhớ công thức hạ bậc lượng giác
Ghi nhớ công thức hạ bậc giúp chúng ta ứng dụng nhanh để giải các bài tập lượng giác. Để ghi nhớ nhanh chông thức hạ bậc trong lượng giác lớp 10 các em học sinh có thể sử dụng mẹo học bằng thơ sau đây:
Sao đi học (ứng dụng vào công thức sin = đối/ huyền)
Cứ khóc hoài (ứng dụng vào công thức cos = kề/ huyền)
Thôi đừng khóc (ứng dụng vào công thức tan = đối/ kề)
Có kẹo đây (ứng dụng vào công thức cot = kề/ đối)
Tìm sin lấy đối chia huyền, cos lấy cạnh kề huyền chia nhau.
Còn tang ta tính như sau: Đối trên, kề dưới chia nhau là ra liền
Cotang cũng rất dễ ăn tiền, kề trên, đối dưới chia liền thể nào cũng ra
2. Công thức cộng lượng giác
Với công thức cộng lượng giác học sinh có thể học mẹo theo cách sau:
Cos (cosin) thì cos cos sin sin, sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng, sin thì giữ dấu xin chàng nhớ cho
Tan (tang) một tổng hai tầng cao rộng, trên thượng tầng tan cộng cùng tan
Hạ tầng số 1 ngang tàng, dám trừ đi cả tan tan oai hùng
Hoặc: Tan tổng thì lấy tổng tan, chia một trừ với tích tan dễ òm
3. Công thức lượng giác biến đổi tổng thành tích
Cách học mẹo với công thức lượng giác biến đổi tổng thành tích:
Cos + cos = 2 cos cos, cos – cos = – 2 sin sin
Sin + sin = 2 sin sin, sin – sin = 2 cos sin
Tan ta + với tan mình = sin hai đứa trên cos mình cos ta
4. Công thức biến đổi tích thành tổng
Với công thức biển tích thành tổng các em có thể học mẹo như sau:
Cos cos nửa cos-cộng
cộng cos-trừ
Sin sin nửa cos-trừ
trừ cos-cộng
Sin cos nửa sin-cộng cộng sin-trừ
5. Công thức lượng giác nhân đôi
Cách học mẹo với công thức lượng giác nhân đôi:
Sin gấp đôi
= 2 sin cos
Cos gấp đôi
= bình cos trừ bình sin
= trừ 1 cộng hai bình cos
= cộng 1 trừ hai bình sin
Từ đây suy ra công thức hạ bậc:
Tan gấp đôi
= Tan đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang ra liền
6. Hàm số lượng giác với các cung đặc biệt
Cách học mẹo hàm số lượng giác với các cung đặc biệt:
Sin bù, Cos đối, Tan (tang) Pi
Phụ nhau Sin Cos, ắt thì phân chia
Hoặc: Cos đối, sin bù, phụ chéo, hơn kém pi tang
Một số dạng bài tập hạ bậc lượng giác
1. Một số lưu ý khi làm bài tập hạ bậc lượng giác
Để giải quyết tốt các bài tập hạ bậc lượng giác, học sinh cần lưu ý:
- Nắm vững và hiểu rõ các công thức hạ bậc lượng giác cơ bản và đạo hàm.
- Áp dụng các công thức vào giải bài tập cần phân tích, chia nhỏ thành các phần nhỏ trong bài và giải quyết từng phần
- Kết hợp các phương pháp tính toán như sử dụng máy tính, tính hoàn toán để đạt kết quả nhanh chóng và chính xác hơn.
2. Luyện tập một số bài tập hạ bậc lượng giác
Bài tập số 1:
Giải phương trình lượng giác: sin2 x = cos2 x + cos2 3x
Đáp án:
Biến đổi phương trình về dạng:
(1 – cos2x)/2 = (1 + cos4x)/2 + cos2.3x
=> 2cos2.3x + (cos4x + cos2x) = 0
=> 2cos23x + 2cos3x . cosx = 0
=> (cos3x + cosx) . cos3x = 0
=> 2cos2x . cosx . cos3x = 0
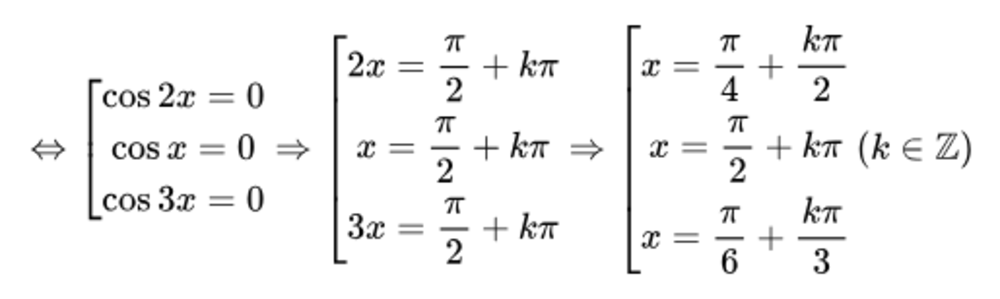
Bài tập số 2:
Chứng minh công thức

Bài tập số 2:
Chứng minh đẳng thức sau
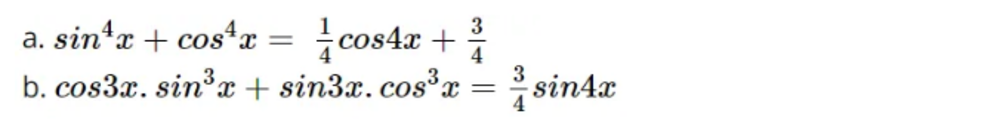
Đáp án:
- Áp dụng công thức hạ bậc ta có:
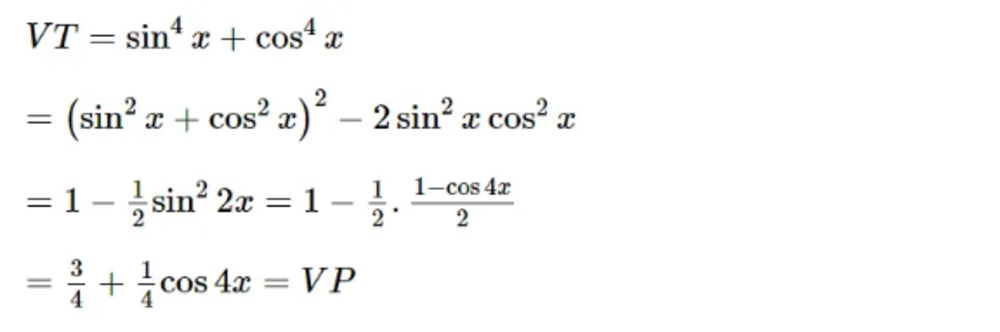
- Ta có
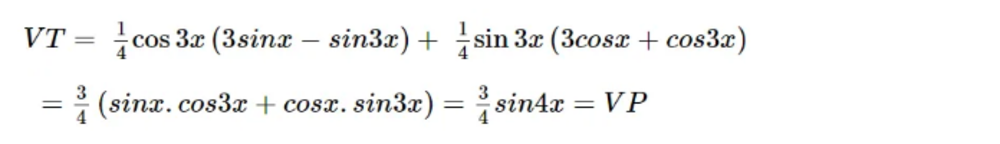
Bài tập số 4:
Giải phương trình lượng giác
- sin3a + cos3a = 0
- sin2a + cos2a = 0
Đáp án:
- Giải phương trình lượng giác:
sin3a + cos3a = 0
=> (1 – cos3a)/2 + cos3a = 0
=> 1 – cos3a + 2cos3a = 0
=> 1 + cos3a = 0
=> cos3a = -1
=> 3a = π + k2π
Vậy nghiệm của phương trình lượng giác này là 3a = π + k2π
- Giải phương trình lượng giác:
sin2a + cos2a = 0
=> (1 – cos2a)/2 + cos2a = 0
=> 1 cos2a + 2cos2a = 0
=> 1 + cos2a = 0
=> cos2a = -1
=> 2a = π + k2π
=> a = π/2 + kπ
Vậy nghiệm của phương trình lượng giác là a = π/2 + kπ
Bài tập số 5:
Rút gọn biểu thức
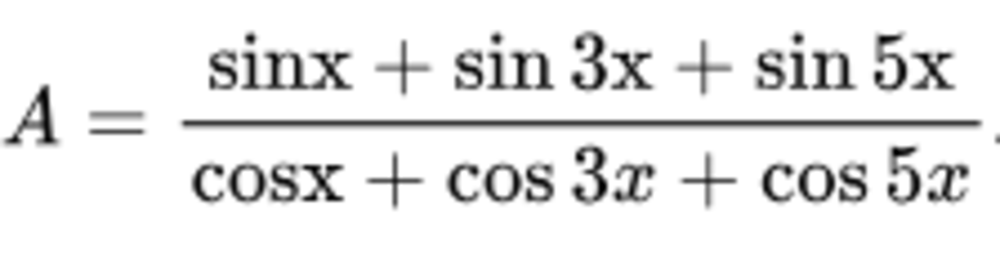
Đáp án:
Áp dụng các công thức:
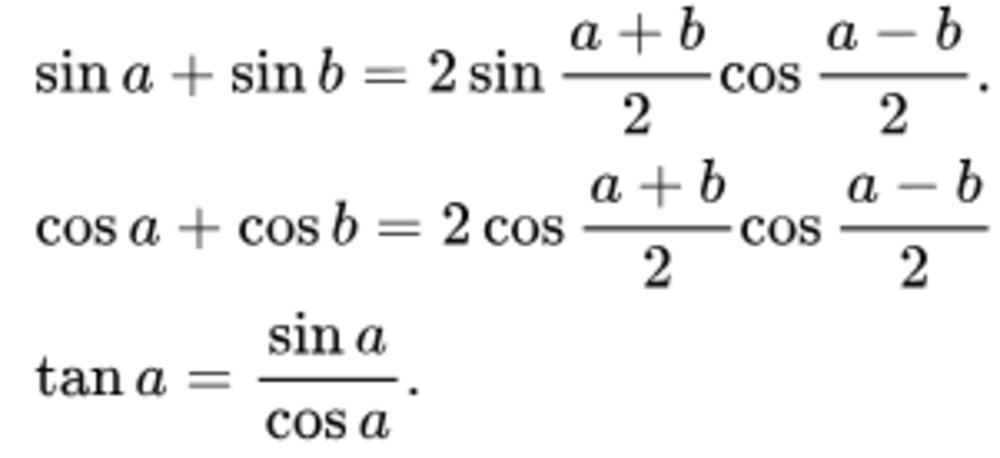
Ta có:
sinx + sin3x + sin5x
= 2sin((5x + x)/2) . cos((5x – x)/2) + sin3x
= 2sin3x cos2x + sin3x
= sin3x(2cos2x + 1) (1)
cosx + cos3x + cos3x
= (cos5x + cosx) cos3x
= 2cos((5x + x)/2) . cos((5x -x)/2)) + cos3x
= 2cos3x . cos2x + cos3x
= cos3x(2cos2x + 1) (2)
Từ (1) và (2) ta có:
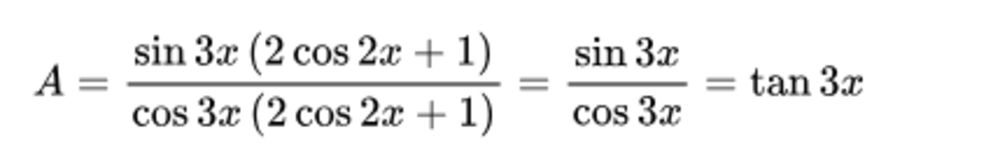
Vậy A = tan3x
Trên đây là 7 công thức hạ bậc lượng giác có bản dành cho học sinh THPT đã được The Dewey Schools tổng hợp đầy đủ. Mặc dù các công thức khá khó nhớ nhưng chỉ cần chăm chỉ ôn luyện các em sẽ nắm vững phần kiến thức này. Hy vọng bài viết này sẽ hữu ích với các bạn đang tìm kiếm thông tin, chúc các em sớm thành thạo kiến thức để áp dụng vào giải các bài tập liên quan nhé.









































