Q là tập hợp số gì? Đây là câu hỏi của rất nhiều bạn học sinh khi bắt đầu tìm hiểu về các tập số trong toán học. Tập hợp Q có vai trò gì và tính chất như thế nào? Các phân loại các tập hợp số chi tiết, chính xác. Tất cả sẽ được giải đáp trong bài viết này. Hãy cùng The Dewey Schools giải đáp mọi thắc mắc.
Q là tập hợp số gì? Ví dụ minh họa
Tập hợp (Q) hay còn gọi là số hữu tỉ là tập hợp của các số thập phân. Tập Q trong toán học là tập hợp các số có thể biểu diễn dưới dạng phân số của hai số nguyên, trong đó mẫu số khác không.
Trong biểu diễn thập phân, các con số sau dấu phẩy được đặt dựa trên các lũy thừa của 10. Ví dụ, 0.25 có thể biểu diễn bằng cách chia 1 cho 4, tức là 0.25 = ¼
Số hữu tỉ là một phần quan trọng trong toán học, và chúng có thể được sử dụng để biểu diễn một loạt các bài tập cụ thể, chẳng hạn như phần trăm, tỉ lệ, và nhiều khái niệm khác liên quan đến quy tắc chia đều một tập hợp thành các phần bằng nhau.
>>Xem thêm: Bảng Chữ Cái Tiếng Việt Chuẩn Nhất Theo Bộ GD&ĐT
Tính chất và phân loại tập hợp số hữu tỉ

Tính chất
Số hữu tỉ có một số tính chất quan trọng và thú vị trong toán học. Dưới đây là một số tính chất chính của số hữu tỉ:
- Phân tích duy nhất: Mọi số hữu tỉ có thể được phân tích duy nhất thành một dãy các số nguyên tương đối nguyên tố (không chia hết cho nhau).
- Phép cộng và trừ: Khi cộng hoặc trừ hai số hữu tỉ, kết quả vẫn là số hữu tỉ.
- Phép nhân: Khi nhân hai số hữu tỉ, kết quả cũng là số hữu tỉ.
- Phép chia: Tuy nhiên, cần lưu ý rằng kết quả của phép chia hai số hữu tỉ không nhất thiết phải là số hữu tỉ. Ví dụ: 2/3 chia cho 5/7 không phải là số hữu tỉ.
- Dạng tối giản: Mỗi số hữu tỉ có thể được biểu diễn dưới dạng phân số tối giản, tức là chia hết cho nhau số nguyên không chia hết.
- Dấu: Số hữu tỉ có thể có dấu dương hoặc âm.
- Bằng nhau nếu và chỉ nếu tương đương: Hai số hữu tỉ a/b và c/d bằng nhau nếu và chỉ nếu (ad = bc).
- Dãy số hữu tỉ liên tiếp: Có vô số số hữu tỉ liên tiếp giữa hai số hữu tỉ bất kỳ.
Những tính chất này giúp chúng ta hiểu và làm việc với số hữu tỉ trong nhiều tình huống khác nhau, từ tính toán đến lý thuyết số.
>>Xem thêm: Chi tiết bảng cửu chương từ 1 đến 10 và mẹo ghi nhớ hiệu quả
Phân loại
Số hữu tỉ có thể được phân loại dựa trên một số thuộc tính khác nhau. Dưới đây là một số cách phân loại phổ biến:
- Dạng tối giản: Số hữu tỉ có thể được phân loại dựa trên dạng tối giản của phân số. Hai phân số có thể có cùng giá trị số hữu tỉ nhưng biểu diễn dưới dạng phân số khác nhau. Ví dụ: 2/3 và 4/6 có cùng giá trị (0.666…), nhưng 2/3 là dạng tối giản.
- Dương và âm: Số hữu tỉ có thể được phân loại thành số dương hoặc số âm dựa trên dấu của chúng. Ví dụ:
- Đơn vị: Số hữu tỉ đơn vị là số hữu tỉ có giá trị tuyệt đối bằng 1. Ví dụ, 5/5 và -7/7 là các số hữu tỉ đơn vị.
- Phân số thập phân hữu hạn và vô hạn: Số hữu tỉ có thể được chia thành hai loại chính dựa trên biểu diễn thập phân của chúng. Số hữu tỉ có biểu diễn thập phân hữu hạn (ví dụ: 3/5 = 0.6) và số hữu tỉ có biểu diễn thập phân vô hạn. Ví dụ: 1/3 = 0.333…
- Số nguyên: Số hữu tỉ cũng có thể là các số nguyên khi tử số chia hết cho mẫu số. Ví dụ: 4/1 = 4
Những cách phân loại này giúp chúng ta hiểu rõ hơn về tính chất và đặc điểm của các số hữu tỉ trong toán học.
>>Xem thêm: [Mới nhất 2023] Số La Mã từ 1 đến 100: Cách đọc, viết chuẩn nhất
Tổng quan về mối quan hệ giữa các tập số trong toán học

Trong toán học, có nhiều tập số khác nhau, và chúng có mối quan hệ đa dạng với nhau. Khi học Toán, bạn cần hiểu được bản chất của từng tập số để áp dụng chúng vào bài tập một cách dễ dàng hơn. Dưới đây là một số mối quan hệ quan trọng giữa các tập số phổ biến:
- Tập số tự nhiên (N) và số nguyên dương (Z﹢): Tập số tự nhiên là tập hợp của các số 0, 1, 2, 3,…, trong khi số nguyên dương chỉ bao gồm các số dương 1, 2, 3,… Nghĩa là tất cả các số trong tập số nguyên dương cũng thuộc tập số tự nhiên.
- Số nguyên (Z) và số nguyên không âm (Z∘⃙): Tập số nguyên bao gồm tất cả các số nguyên dương, số 0 và các số nguyên âm. Tập số nguyên không âm chỉ bao gồm số 0 và tất cả các số nguyên dương. Nghĩa là tập số nguyên không âm là một phần của tập số nguyên.
- Số hữu tỉ (Q) và số nguyên (Z): Tập số hữu tỉ là tập hợp của tất cả các số có thể biểu diễn dưới dạng phân số của hai số nguyên, trong đó mẫu số khác 0. Tập số nguyên là một phần của tập số hữu tỉ, vì mọi số nguyên có thể được biểu diễn dưới dạng phân số với mẫu số bằng 1.
- Số thực (R) và số hữu tỉ (Q): Tập số thực bao gồm tất cả các số có thể được biểu diễn trên trục số thực, bao gồm cả các số hữu tỉ và vô tỉ. Tập số hữu tỉ chỉ là một phần rất nhỏ của tập số thực, vì các số thực vô tỉ như căn bậc hai của 2 không thể biểu diễn dưới dạng số hữu tỉ.
- Số phức (C) và số thực (R): Tập số phức bao gồm tất cả các số có dạng (a + bi), trong đó (a) và (b) là các số thực và (i) là đơn vị ảo thỏa mãn (i^2 = -1). Tập số thực là một phần của tập số phức, với (b) trong dạng số phức có thể bằng 0.
Những mối quan hệ này thể hiện cách các tập số trong toán học liên kết và gắn kết với nhau, tạo nên một cơ sở chặt chẽ cho việc nghiên cứu và ứng dụng trong nhiều lĩnh vực khác nhau.
Số vô tỉ là gì? Phân biệt số hữu tỉ và số vô tỉ

Số vô tỉ là gì?
Số vô tỉ (kí hiệu là I) là một loại số không thể biểu diễn dưới dạng phân số của hai số nguyên. Nghĩa là không có cách nào biểu diễn chính xác một số vô tỉ bằng một tỷ số của hai số nguyên. Số vô tỉ có dạng thập phân vô hạn và không lặp đi lặp lại theo một mẫu nào đó.
Ví dụ về số vô tỉ là √2. Số này không thể biểu diễn dưới dạng phân số của hai số nguyên, và biểu diễn thập phân của nó là một dãy số vô hạn không lặp lại:1.41421356237….
Ngoài căn bậc hai của 2, còn rất nhiều số vô tỉ khác như (số Pi),(số Euler), căn bậc ba của 3 và nhiều hằng số và căn bậc n của các số nguyên khác. Số vô tỉ là một phần quan trọng của tập số thực R và có những đặc điểm độc đáo và thú vị trong toán học.
Phân biệt số hữu tỉ và số vô tỉ
Số hữu tỉ (Q) và số vô tỉ (I) là hai loại số khác nhau trong toán học. Dưới đây là cách phân biệt giữa chúng:
- Định nghĩa
- Số hữu tỉ là số có thể biểu diễn dưới dạng phân số của hai số nguyên, trong đó mẫu số khác 0.
- Số vô tỉ là số không thể biểu diễn dưới dạng phân số của hai số nguyên.
- Biểu diễn thập phân
- Số hữu tỉ có biểu diễn thập phân hữu hạn hoặc lặp lại chu kỳ.
- Số vô tỉ có biểu diễn thập phân vô hạn không lặp lại.
- Phân số tối giản
- Số hữu tỉ có thể được biểu diễn dưới dạng phân số tối giản, tức là không còn cách nào chia tử số và mẫu số chung lớn hơn 1.
- Số vô tỉ không thể biểu diễn dưới dạng phân số tối giản.
- Ví dụ
- 5/3 là một số hữu tỉ.
- √2 là một số vô tỉ.
Tóm lại, sự chênh lệch cơ bản giữa số hữu tỉ và số vô tỉ nằm ở khả năng biểu diễn dưới dạng phân số của hai số nguyên. Số hữu tỉ có thể biểu diễn như vậy, trong khi số vô tỉ không thể.
Các dạng bài tập thông dụng về số hữu tỉ
Để học thành thạo về số hữu tỉ, bạn cần hiểu về tập số này và cần tìm hiểu nhiều dạng bài về số hữu tỉ. Sau đây, TDS sẽ giúp bạn tổng hợp một số dạng bài thông dụng về số hữu tỉ
Phép tính cộng trừ nhân chia thường gặp
Dưới đây là một số ví dụ về phép tính cộng, trừ, nhân và chia các số hữu tỉ:

Biểu diễn số hữu tỉ trên trục số
Biểu diễn số hữu tỉ trên trục số thực là cách thể hiện các số hữu tỉ trên một đường thẳng số thực. Các số hữu tỉ được biểu diễn bằng các điểm trên trục số, sắp xếp theo thứ tự tăng dần hoặc giảm dần. Dưới đây là ví dụ về cách biểu diễn số hữu tỉ trên trục số:
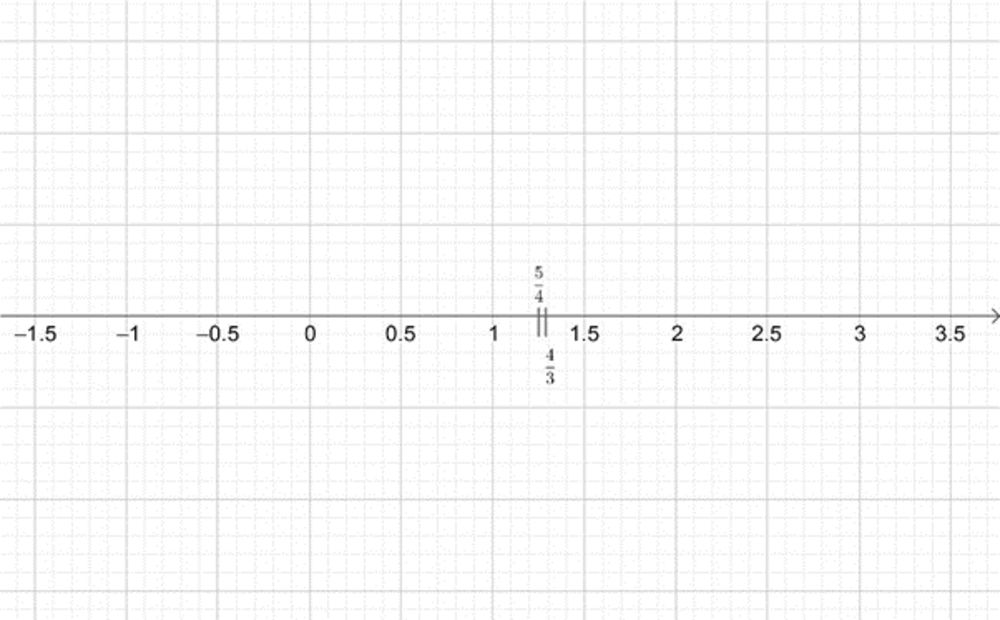
Biểu diễn số hữu tỉ trên trục số giúp bạn hình dung cách các số hữu tỉ liên quan đến nhau và cách chúng phân bố trên trục số thực.
So sánh 2 số hữu tỉ với nhau
Để so sánh hai số hữu tỉ với nhau, bạn có thể sử dụng các phép tính cơ bản như cộng, trừ, nhân và chia để so sánh giá trị của chúng.
- So sánh bằng nhau: Để xác định xem hai số hữu tỉ có bằng nhau hay không, hãy so sánh giá trị của chúng bằng cách thực hiện phép tính trừ và kiểm tra xem kết quả có bằng 0 hay không. Ví dụ: 3/4 và 6/8 bằng nhau vì 3/4 – 6/8 = 0
- So sánh theo kích thước: Để xác định số hữu tỉ nào lớn hơn trong hai số, bạn có thể so sánh tỷ lệ giữa chúng. Cách này thường dùng để so sánh hai số dương hoặc hai số âm.
- So sánh theo biểu diễn thập phân: Nếu cần, bạn có thể biểu diễn cả hai số hữu tỉ dưới dạng thập phân để dễ dàng so sánh. Sau đó, so sánh các dãy số thập phân tương ứng của chúng.
Nhớ kiểm tra đúng dấu của các số hữu tỉ khi bạn so sánh chúng (dương hoặc âm), và cẩn thận trong việc làm tròn số thập phân để tránh sai sót trong quá trình so sánh.
Tìm số hữu tỉ nằm trong một khoảng cho trước
Để tìm số hữu tỉ nằm trong một khoảng cho trước, bạn có thể sử dụng một loạt các phương pháp. Dưới đây là một số cách thường được sử dụng:
1. Sử dụng phân số gần đúng
Bắt đầu bằng cách xác định phân số gần đúng nằm trong khoảng đã cho. Ví dụ, nếu bạn muốn tìm số hữu tỉ nằm giữa 1 và 2, bạn có thể chọn phân số 3/2
2. Sử dụng phân loại số hữu tỉ theo dãy số
– Biểu diễn các số hữu tỉ trên trục số thực.
– Xác định khoảng nào trên trục số thực chứa khoảng mà bạn muốn tìm số hữu tỉ.
– Tìm số hữu tỉ cận trên và cận dưới của khoảng này bằng cách sử dụng các số hữu tỉ gần nhất từ trên và dưới trục số.
3. Sử dụng tìm kiếm nhị phân
– Đặc biệt hiệu quả khi bạn muốn tìm một số hữu tỉ trong một khoảng nhỏ.
– Chia khoảng cần tìm thành các khoảng con nhỏ hơn, sau đó kiểm tra xem số hữu tỉ nằm ở khoảng con nào.
– Lặp lại quá trình trên cho các khoảng con liên tiếp cho đến khi bạn xác định được số hữu tỉ mong muốn.
4. Sử dụng thuật toán liên quan đến số hữu tỉ
– Có một số thuật toán liên quan đến số hữu tỉ như thuật toán tìm gần đúng bằng phân chia.
– Tùy thuộc vào yêu cầu và mức độ chính xác, bạn có thể áp dụng các thuật toán này để tìm số hữu tỉ trong khoảng cụ thể.
Tìm điều kiện để số hữu tỉ là dương, âm hoặc bằng 0
Để tìm điều kiện để một số hữu tỉ là dương, âm hoặc bằng 0, bạn cần xem xét dấu của tử số và mẫu số trong phân số. Dưới đây là cách xác định điều kiện cho từng trường hợp:
1. Số hữu tỉ dương: Một số hữu tỉ là dương nếu cả tử số và mẫu số đều dương.
2. Số hữu tỉ âm: Một số hữu tỉ là âm nếu tử số là âm và mẫu số là dương, hoặc tử số là dương và mẫu số là âm.
3. Số hữu tỉ bằng 0: Một số hữu tỉ bằng 0 nếu tử số bằng 0.
Các bài toán tìm x với số hữu tỉ từ cơ bản đến nâng cao
Để giải một bài toán tìm giá trị của biến (x) trong phạm vi các số hữu tỉ, bạn cần xây dựng phương trình hoặc bất phương trình dựa trên yêu cầu của bài toán và sau đó giải phương trình hoặc bất phương trình đó để tìm giá trị của (x). Dưới đây là một số ví dụ về cách giải các bài toán này:

Bài tập ví dụ về số hữu tỉ kèm lời giải chi tiết
Để hiểu rõ hơn về các dạng bài tập số hữu tỉ Q, bạn cần áp dụng vào các bài toán cụ thể. Dưới đây là một số bài tập điển hình thường gặp, bạn hãy chép lại đề bài và tự giải chúng. Nếu có khó khăn, hãy tham khảo lời giải mà chúng tôi đã đề xuất ở dưới!
Bài tập 1: Dạng bài cộng trừ nhân chia số hữu tỉ

Bài tập 2: Bài tập so sánh hai số hữu tỉ

Bài tập 3: Bài tập tìm x và tìm điều kiện thỏa mãn số hữu tỉ dương

Chắc hẳn bạn đã có câu trả lời cho câu hỏi “Q là tập hợp số gì?” sau khi đọc bài viết này. Đây là một tập hợp số rất quan trọng trong Toán học mà bạn sẽ làm quen trong chương trình lớp 7 và sẽ theo bạn ở những bậc cao hơn. Do đó, bạn cần ghi nhớ và học tập nhiều hơn về tập hợp số này. The Dewey Schools chúc bạn có những giờ học hiệu quả, năng suất và vui vẻ. Đừng quên theo dõi chúng tôi để có nhiều thông tin bổ ích hơn.









































